Implementation details¶
This section describes the technical details of the simulation flow for a standard model component and for the conversion of a Chandra observation. In order to take advantage of the efficient array manipulation capabilities provided by numpy, the entire implementation is vectorized, i.e. we don’t have an explicit event loop in python.
Standard model component¶
The basic flow of the simulation for a single standard model component is coded
in ixpeobssim.srcmodel.roi.xModelComponentBase.rvs_event_list().
Mathematically speaking, the simulation algorithm can be spelled out in the form
of the following basic sequence:
Given the source spectrum
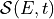 and the effective area
and the effective area
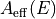 , we calculate the count spectrum as a function of
the energy and time:
, we calculate the count spectrum as a function of
the energy and time:![\mathcal{C}(E, t) = \mathcal{S}(E, t) \times A_{\rm eff}(E)
\quad [\text{s}^{-1}~\text{keV}^{-1}].](_images/math/f8af2e8ab8cb6411b9554c09559d89a4b7baf644.png)
In case of a source with cosmological redshift
 or hydrogen column
density
or hydrogen column
density 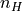 different from zero, these two quantities are used to
correctly re-scale
different from zero, these two quantities are used to
correctly re-scale 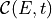 :
: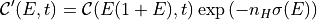
We calculate the light curve of the model component (in counts space) by integrating over the energy:
![\mathcal{L}(t) = \int_{E_{\rm min}}^{E_{\rm max}} \mathcal{C}'(E, t) dE
\quad [\text{Hz}].](_images/math/c537858d3e8d19e9d894e78406e1ff117a5d524b.png)
We calculate the total number of expected events
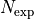 by
integrating the count rate over the observation time:
by
integrating the count rate over the observation time: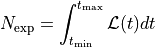
and we extract the number of observed events
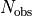 according
to a Poisson distribution with mean
according
to a Poisson distribution with mean 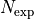 .
.We treat the count rate as a one-dimensional probability density function in the random variable
 , we extract a vector
, we extract a vector  of
of 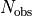 values of
values of  according to this pdf—and we
sort the vector itself. (Here and in the following we shall use the hat
to indicate vectors of lenght
according to this pdf—and we
sort the vector itself. (Here and in the following we shall use the hat
to indicate vectors of lenght 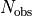 .)
.)We treat the array of count spectra
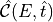 ,
evaluated at the time array
,
evaluated at the time array  , as an array of one-dimensional
pdf objects, from which we extract a corresponding array
, as an array of one-dimensional
pdf objects, from which we extract a corresponding array 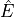 of
(true) energy values. (In an event-driven formulation this would
be equivalent to loop over the values
of
(true) energy values. (In an event-driven formulation this would
be equivalent to loop over the values 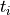 of the array
of the array
 , calculate the corresponding count spectrum
, calculate the corresponding count spectrum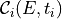
and treat that as a one-dimensional pdf from which we extract a (true) energy value
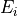 , but the vectorized description is more germane to what
the code is actually doing internally.)
, but the vectorized description is more germane to what
the code is actually doing internally.)We treat the energy dispersion
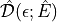 as an array of one-dimensional pdf objects that we use to extract
the measured energies
as an array of one-dimensional pdf objects that we use to extract
the measured energies 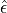 and the corresponding
PHA values.
and the corresponding
PHA values.We extract suitable arrays of (true)
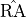 ,
,
 values and, similarly to what we do with the energy
dispersion, we smear them with the PSF in order to get the correponding
measured quantities.
values and, similarly to what we do with the energy
dispersion, we smear them with the PSF in order to get the correponding
measured quantities.We use the polarization degree
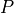 and angle
and angle 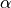 of the
model component to calculate the visibility
of the
model component to calculate the visibility 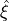 and the phase
and the phase
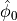 of the azimuthal distribution modulation, given the
modulation factor
of the azimuthal distribution modulation, given the
modulation factor 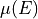 of the polarimeter
of the polarimeter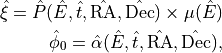
and we use these values to extract the directions of emission of the photoelectron.
(For periodic sources all of the above is done in phase, rather than in time, and the latter is recovered at the very end using the source ephemeris, but other than that there is no real difference.)
For source models involving more than one component, this is done for each component separately, and the different resulting phothon lists are then merged and ordered in time at the end of the process.
Conversion of a Chandra observation¶
In this case the starting point is a Chandra photon list, publicly available on
the on-line database, which includes
temporal, energetic and spatial information for each detected event.
Being the Chandra angular and energetic resolution (respectively HPD
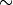 1 arcsec and FWHM
1 arcsec and FWHM 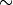 5% at 5.9 keV) much better
than those expected for the IXPE mission), energies
5% at 5.9 keV) much better
than those expected for the IXPE mission), energies 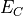 and positions
and positions
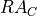 ,
, 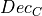 measured by Chandra can be assumed as Monte
Carlo truth.
measured by Chandra can be assumed as Monte
Carlo truth.
From the implementation standpoint, the conversion is coded
in ixpeobssim.srcmodel.roi.xChandraObservation.rvs_event_list() and
can be summarized in the following steps:
We compute the ratio
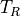 between the Chandra observation time
between the Chandra observation time
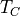 and the provided IXPE simulation time
and the provided IXPE simulation time 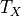 :
: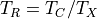
We scale Chandra detected events by first concatenating the measured arrays (
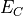 ,
, 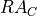 and
and 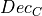 ) as many times as the integer
part of
) as many times as the integer
part of 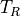 (denoted
(denoted 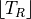 ) and then appending
to the end of the sequence a portion whose relative length is equal to the
fractional part of
) and then appending
to the end of the sequence a portion whose relative length is equal to the
fractional part of 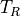 (called
(called 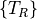 ).
For instance, in case of the energy:
).
For instance, in case of the energy:
We calculate the effective area ratio
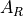 between one IXPE telescope
and Chandra as a function of energy and off-axis angle
between one IXPE telescope
and Chandra as a function of energy and off-axis angle 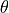 :
: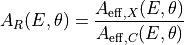
This ratio allows to conveniently down-sample the Chandra time-scaled photon list. In practice, this is done by throwing an array of random numbers
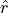 between 0 and 1, and accepting as IXPE events only those
that meet the condition:
between 0 and 1, and accepting as IXPE events only those
that meet the condition: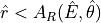
We randomly extract the event times
 uniformly between the
starting and ending observation time.
uniformly between the
starting and ending observation time.From this point, once the arrays
 ,
,  ,
,
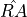 and
and 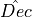 of true values are selected,
the simulation goes ahead as in the standard model component case.
In particular, we smear these quantities with the IXPE response functions
and we extract the emission angle
of true values are selected,
the simulation goes ahead as in the standard model component case.
In particular, we smear these quantities with the IXPE response functions
and we extract the emission angle  based on the input
polarization model.
based on the input
polarization model.
In case of definition of multiple sub-regions of the ROI, the conversion is done separately for each of them (skipping those flagged as to be removed), and the resulting photon lists are merged and ordered in time at the end of the process.
